1. What is Volume?
Volume is defined as the amount of space taken up by an object of three dimensions. It is measured in cubic units. Some of the common units of volume are m³ and cm³. If you take a glass and fill it completely with water, the amount of water present in the glass is the volume of the glass.
All 3D shapes have a volume which can be calculated using the formula specified for that shape. The general idea to workout the volume of any 3D shape is: area of cross section times height.
Let us learn the formulas for the volumes of 3D Shapes covered in 11 plus examinations.
1.1 Cube: Volume formula and solved example
Cube is one of the simplest three-dimensional shapes with all the dimensions of the same size. It has six-square faces, eight vertices, and twelve edges.
All the six faces of cubes are squares, a two-dimensional face.
For a cube of side a,

Using the general idea of volume as the area of cross section × height,
For cube, area of cross section = area of square
Volume of cube = Area of square face × height
= a² × a
Volume of cube = a³
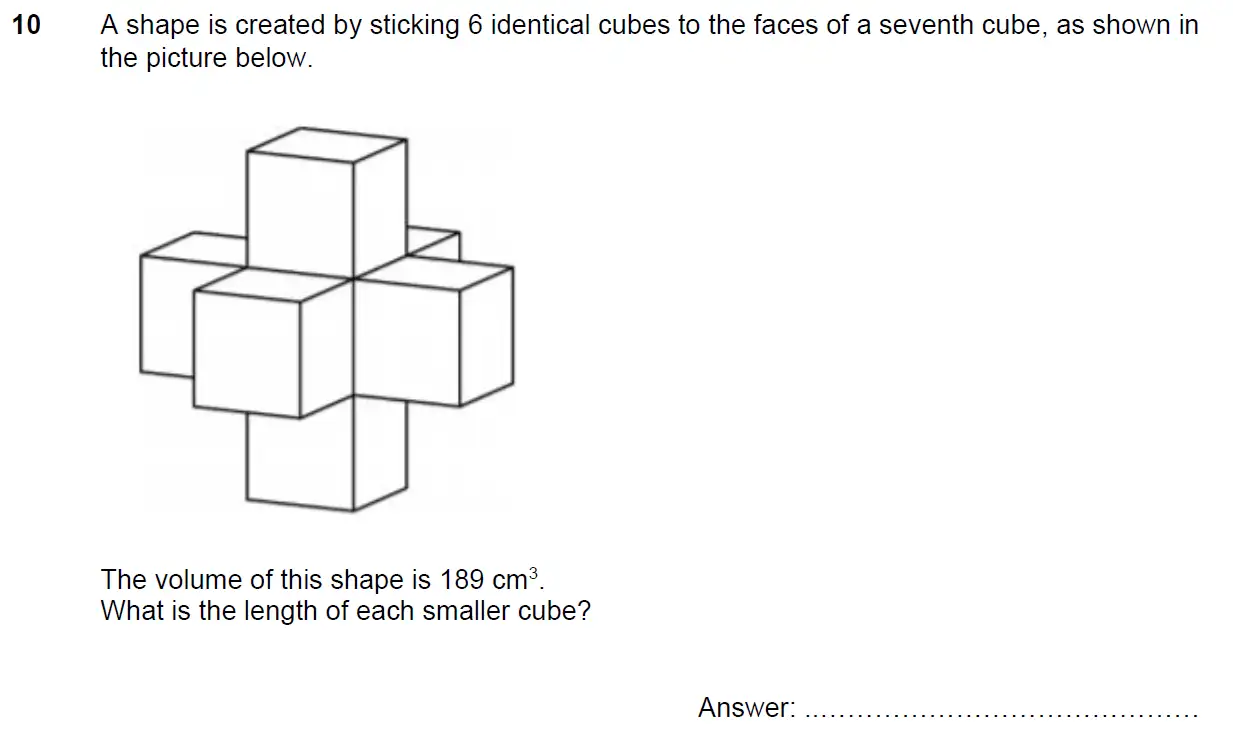
Example: A wooden cubic box has a volume of 64 cm³. Work out the side length of the box.
Solution: Let a be the side length of the cubic box.
Volume of cube = a³
So, a³ = 64
a × a × a = 4 × 4 × 4
a = 4 cm
The side length of the box is 4 cm
1.2 Cuboid: Volume formula and solved example
A cuboid is a three-dimensional shape with the dimensions as length, width, and height. It has six rectangular faces, eight vertices, and twelve edges.
Let l,w and h be the length, width, and height of the cuboid respectively.

Using the general idea of volume as the area of cross-section × height,
For the cuboid, area of cross-section = area of rectangle
Volume of cuboid
= Area of rectangle × height
Volume of cuboid = l × w × h
Example: The base of Sarah’s fish tank is 60 cm long and 20 cm wide. If the height of the fish tank is 30 cm, what is the maximum volume of water the tank can hold?
Solution: Maximum volume of water in the tank is the tank’s volume
The tank is in a cuboid shape.
Length of tank (l) = 60 cm
Width of tank (w) = 20 cm
Height of tank (h) = 30 cm
Volume of cuboidal fish tank = l × w × h
= 60 × 20 × 30
= 36000 cm³
Maximum volume of water the tank can hold is 36000 cm³.
2. Volume of Prisms
Prisms are 3D shapes which have the same face on both the ends. It has a constant area of cross-section throughout.
2.1 Finding the volume of a triangular prism.
A triangular prism is a 3D shape consisting of two triangular ends connected by three rectangles. The triangular ends of a triangular prism are exactly the same.

We can calculate the volume of this triangular prism by simply multiplying the area of one triangle with the prism's height.
The volume of triangular prism = Area of triangle × height of prism
Example 1: Calculate the volume of the triangular prism shown below.

Solution: Volume of triangular prism = Area of triangle × height of prism
Area of triangle = 1⁄2 × base × height
= 1⁄2× 9 × 5
= 45⁄2
= 22.5 in²
Volume of triangular prism = 22.5 × 15 = 337.5 in³
Example 2: Work out the volume of the pentagonal prism shown below.
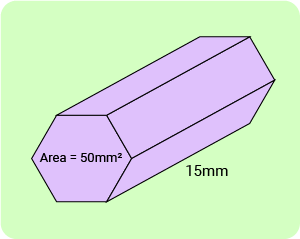
Solution: Volume of pentagonal prism = Area of pentagon × height of prism
Area of pentagon = 50 mm²
Volume of pentagonal prism = 50 × 15
= 750 mm³
Now think about prisms that have rectangular faces at both the ends. Such prisms are called rectangular prisms. Rectangular prisms are nothing but cuboids and so the volume of rectangular prisms is equal to the volume of cuboids.