

GCSE Solved Topic Wise Questions
5320+
Students
70% OFF
£79
Add to Basket
- Practice 5K+ topic-wise questions, tagged by difficulty and time.
- Unlock instantly, 2026, GCSE exams, 150+ Maths Past & Predicted Papers.
- Access detailed step-wise solutions by GCSE examiners on the website.
- Get full GCSE Maths exam syllabus & download paper planner.
- Boost exam speed, accuracy, & confidence for GCSE exams.
- Suitable for Edexcel, AQA, OCR, WJEC, CCEA & Eduqas boards.
70% OFF
£79
Add to Basket
GCSE Exam Topics
Laws of Indices - GCSE Maths Exam Questions & Answers
Use Calculator :No

Use Calculator :No
4:00
Topics Covered:
Topics Covered:
Use Calculator :Yes

Use Calculator :Yes
2:00
Topics Covered:
Topics Covered:
Use Calculator :No

Use Calculator :No
1:30
Topics Covered:
Topics Covered:
Use Calculator :Yes

Use Calculator :Yes
2:30
Topics Covered:
Topics Covered:
Use Calculator :No

Use Calculator :No
1:00
Topics Covered:
Topics Covered:
Use Calculator :No
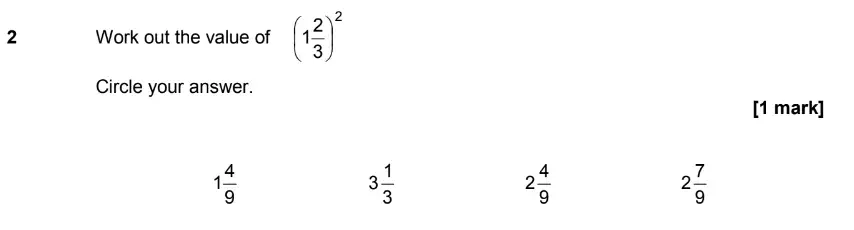
Use Calculator :No
1:30
Topics Covered:
Topics Covered:
Use Calculator :Yes
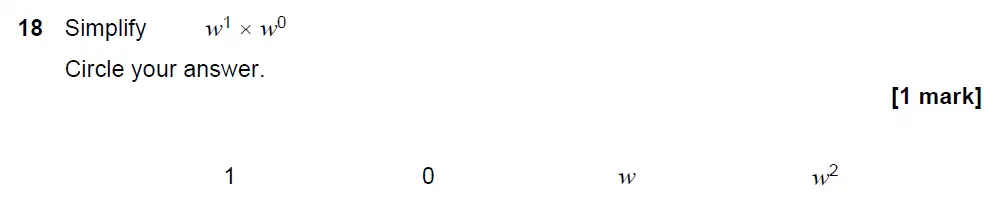
Use Calculator :Yes
0:30
Topics Covered:
Topics Covered:
Use Calculator :Yes

Use Calculator :Yes
3:00
Topics Covered:
Topics Covered:
Use Calculator :No
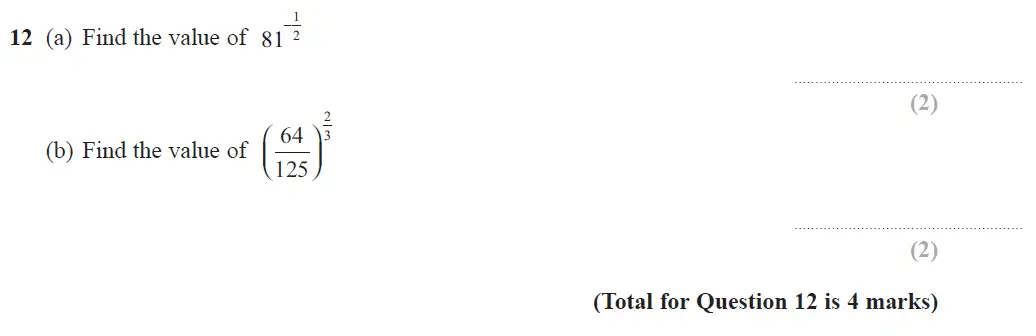
Use Calculator :No
2:30
Topics Covered:
Topics Covered:
Use Calculator :No
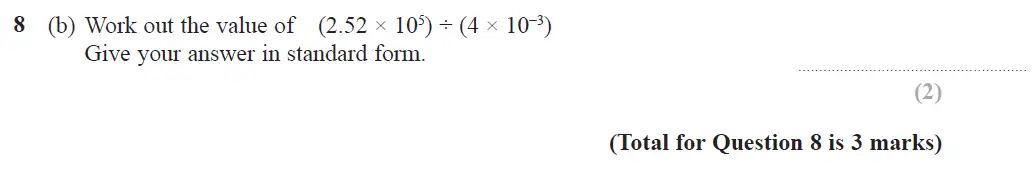
Use Calculator :No
2:00
Topics Covered:
Topics Covered:


